What is Recursion? Types of Recursion
Recursion in C Language
Recursion in C or in any other programming language is a programming technique where a function calls itself certain number of times. A function which calls itself is called a recursive function, the call is recursive call and the process of function implementation is recursion.
Formally, Recursion is a programming technique that comes from recurrence relation, where the problem is divided further in sub problems smaller in size but same in nature. This division stops when the problem cannot be divided further. This point is called base case from where control moves back towards the original problem by solving sub problems and assembling results in order to get the final result.
Recursion in C - A Working Example
While studying recursion in C, if you are asked to write a function void printBin(int n), which takes a decimal integer as an argument, and prints it's binary form on screen. You can think of two implementations of this function. First version is an iterative one that stores binary digits in an array as they are produced then prints the array content in reverse order. The second one is a recursive version void recPrintBin(int n). Recursive version recPrintBin calls itself by passing n/2 to the subsequent calls until n is either 1 or zero, then start printing n%2 from the stack of calls, and solves the problem recursively.
Below piece of code is the iterative version (void printBin(int n)) of decimal to binary conversion. In this implementation we first get the number converted in 1's and 0's but not in right order, so to print the string of binary digits in correct order string binS first needs to be reversed, and then printed.
/* File: dec_to_bin.c Program: decimal to binary conversion of positive integer (iterative version) */ #include <stdio.h> #include <string.h> void printBin (int); void reverse(char *); int main () { printf("Binary of 19 is: "); printBin(19); printf("\n"); } void printBin (int n) { char binS[256]; //contains binary digits. int i = 0; do { binS[i++] = n % 2 + '0'; } while (n/=2); binS[i] = '\0'; //null at the end of string reverse (binS); //reverse the order of 1's and 0's printf ("%s\n", binS); } /* helper function to reverse a string */ void reverse (char *s) { int lastIndex = strlen(s) - 1; int firstIndex = 0; char ch; while (firstIndex < lastIndex) { ch = s[firstIndex]; s[firstIndex] = s[lastIndex]; s[lastIndex] = ch; firstIndex++; lastIndex--; } } OUTPUT ====== Binary of 19 is: 10011
Now, see the recursive version of the same problem.
/* Demonstration of Recursion in C File: rec_dec_to_bin.c Program: decimal to binary conversion of positive integer (recursive version) */ #include <stdio.h> #include <string.h> void recPrintBin (int); int main () { int n; printf("Enter an integer: "); scanf("%d", &n); printf("Recursively computed binary of %d is: ", n); recPrintBin(n); printf("\n"); } void recPrintBin (int n) { if (n == 1 || n == 0) //base case { printf ("%d", n); return; } recPrintBin (n/2); //recursive call printf("%d", n%2); } OUTPUT ====== Enter an integer: 19 Recursively computed binary of 19 is: 10011
From above pieces of codes, it can be clearly seen that the second piece of code is more concise and cleaner. However, application of recursion is completely problem dependent and it may not be suitable for all problem types.
If you analyze decimal to binary conversion problem, you will find that in the first solution (iterative one), the binary-digit generated in the last iteration should be printed first. That's the reason character array binS needed to be reversed before printing on console.
On the contrary, the recursive version does not need any reverse of binary digits because in recursion, the very last call to function is processed very first, then second last and so on. This is done with help of a stack of calls, where the last call to function is placed on top of the stack, therefore processed first. That's how recursion in C is tackled and processed.
There are some classical examples which can be better implemented using recursion rather than their iterative counterparts. Towers of Hanoi, recursive listing of directories or folders and Russian Matryoshka dolls are some of them.
How does Recursion Work in C Program?
A recursive function has following two parts:
1. The base case
2. Recursive call
Base case is the case for which the function is evaluated without recursion. In above example the base case is if(n == 1 || n == 0), which prints value of n without making any subsequent recursive call. Recursive call is the central part of a recursive function and during each call parameter values come closer to the base case. And, when the base case is reached it is evaluated without recursion and results are returned to the previous call, then from previous to previous and so on, until the function reaches to its caller.
Types of Recursion
A function is recursive if it makes a call to itself directly or indirectly. If a function f() calls itself within from its own body, it is called recursive. Secondly, if a function f() calls another function g() that ultimately calls back to f(), then it can also be considered a recursive function. Following variants of recursion tell us making recursive calls in different ways depending upon the problem.
Linear Recursion
In linear recursion a function calls exactly once to itself each time the function is invoked, and grows linearly in proportion to the size of the problem. Finding maximum among an array of integers could be a good example of linear recursion. The same is demonstrated below:
Let's assume that we are given an array arr of n decimal integers and we have to find the maximum element from the given array. We can solve this problem using linear recursion by observing that the maximum among all integers in arr is arr[0], if n==1, or the maximum of first n-1 in arr and the last element in arr.
/* File: rec_max_array.c Program: Find maximum among array elements recursively. */ #include <stdio.h> #define SIZE 10 int recursiveMax (int *, int ); int max (int, int); int main () { int arr[SIZE] = {1, 3, 5, 4, 7, 19, 6, 11, 10, 2}; int max = recursiveMax(arr, SIZE); printf("Maximum element among array items is: %d\n", max); } int recursiveMax (int *arr, int n) { if (n == 1) return arr[0]; return max (recursiveMax (arr, n-1), arr[n-1]); } /* helper function to compute max of two decimal integers */ int max (int n, int m) { if (n > m) return n; return m; } OUTPUT ====== Maximum element among array items is: 19
Tail Recursion
Tail Recursion is another form of linear recursion, where the function makes a recursive call as its very last operation. Note that, there is a difference between last operation and last statement. If you see at recursiveMax (defined above), then you will find that recursive call to function recursiveMax is last statement but not last operation, code arr[n-1] yet to be processed to complete the execution of last statement.
Therefore, a function will be said tail recursive if the recursive call is the last thing the function performs. When a function uses tail recursion, it can be converted to the non-recursive one, by iterating through the recursive calls rather than calling them explicitly. Reversing array elements could be a good example of tail recursion. The recursive solution of reversing array elements problem is illustrated as below, followed by it's iterative version.
Suppose, we are given an array of decimal integers, and we have to reverse the order of elements in which they are stored. We can solve this problem by using linear recursion. Reversal of an array can be achieved by swapping the first and last elements and then recursively reversing the remaining elements in the array.
/* File: rec_array_reverse.c Program: Reverse array elements recursively. */ #include <stdio.h> #define SIZE 10 void recursiveRev (int *, int, int); int main () { int arr[SIZE] = {1, 2, 3, 4, 5, 6, 7, 8, 9 , 10}; int i; recursiveRev (arr, 0, SIZE-1); printf ("Printing array elements after reversing them...\n"); for (i = 0; i < SIZE; i++) printf ("%d\n", arr[i]); } void recursiveRev (int * arr, int i, int j) { if(i < j) { int tmp; tmp = arr[i]; arr[i] = arr[j]; arr[j] = tmp; recursiveRev (arr, i+1, j-1); } } OUTPUT ====== Printing array elements after reversing them... 10 9 8 7 6 5 4 3 2 1
Recursive version of reversing array elements problem can easily be converted into iterative one as follows:
void iterativeRev (int *arr, int n) { int i = 0, j = n - 1; int tmp; while (i < j) { tmp = arr[i]; arr[i] = arr[j]; arr[j] = tmp; i++; j--; } }
But, if you look at the signatures of recursiveRev and iterativeRev you will find a little difference there, both functions are passed different number of arguments. It is so, because to facilitate recursion sometimes the problem may need to be redefined.
Binary Recursion
As name suggests, in binary recursion a function makes two recursive calls to itself when invoked, it uses binary recursion. Fibonacci series is a very nice example to demonstrate binary recursion. See the example below:
fib (1) = fib (2) = 1
fib (n) = fib (n-1) + fib (n-2), if n > 2
By definition, the first two numbers in the Fibonacci sequence are 0 and 1, and each subsequent number is the sum of the previous two [Definition Source wikipedia].
/* File: bin_rec_fib.c Program: Computes n-th fibonacci number using binary recursion. */ #include <stdio.h> int recursiveFib (int); int main () { int n = 6; printf ("%dth fibonacci number is %d\n", n, recursiveFib(n)); } int recursiveFib (int n) { // base case if (n <= 1) return n; // binary recursive call return recursiveFib(n-1) + recursiveFib (n - 2); } OUTPUT ====== 6th fibonacci number is 8
Above piece of code exercises binary recursion in order to compute 6th fibonacci number. In this piece of code recursiveFib returns n in case n is less than or equal to 1. This is the base condition in recursiveFib from where recursive call returns to previous call. Following figure shows how recursiveFib is executed.
Multiple Recursion
Multiple recursion can be treated a generalized form of binary recursion. When a function makes multiple recursive calls possibly more than two, it is called multiple recursion.
How to Trace Recursive Calls?
When a function is called recursively, each call gets a fresh copy of all local/automatic variables. And every call is saved in a stack, where the last most call will be processed first. Every program maintains a stack (a special area of memory) during run time to remember where to go back when a function is called.
You can trace a recursive function by pushing every call it makes to a stack and then come to the previous call when it returns. Look at the following piece of code and try to trace it; we will do in a moment's time.
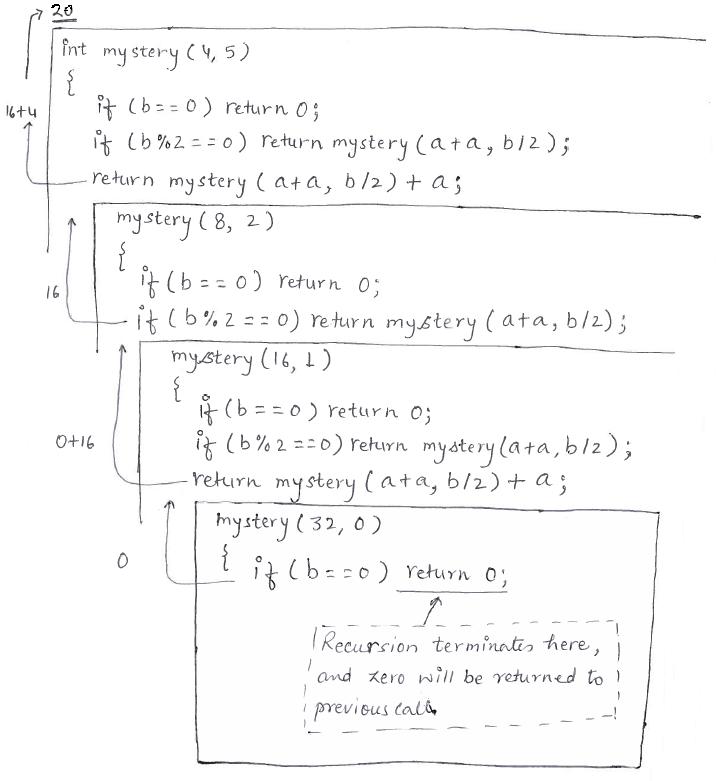
#include <stdio.h> int mystery (int a, int b) { if (b == 0) return 0; if (b % 2 == 0) return mystery (a+a, b/2); return mystery (a+a, b/2) + a; } int main() { int i = 4, j = 5; printf("mystery of %d and %d is: %d\n", i, j, mystery (4, 5)); } OUTPUT ====== mystery of 4 and 5 is: 20
In below figure, I represent each call with a concentric box, where inner boxes will represent the deeper level of recursion. As you see, in the innermost box recursion terminates and no further recursive call is made. And, it starts returning to parent calls ladder by ladder.
Pros and Cons of Recursion
The main advantage recursion provides to programmers is that it takes less code to write comparative to iterative version. The code written with help of recursion is more concise, cleaner and easier to understand.
There are some data structures you will see which are quite easy to code with help of recursion. Tree traversals, quick, and merge sort are a few examples.
Despite above benefits, recursion provides no storage saving, nor time. As we have discussed that every recursive call is saved in a special memory area the program maintains (i.e., stack). Pushing a call frame to stack and removing it back is time consuming relative to the record keeping required by iterative solution. There may be chances your recursive solution results into Stack overflow, in case the number of recursive calls does not fit into the stack.
Conclusion - Recursion
Hope you have enjoyed reading Recursion in C. Having seen at pros and cons of recursion, you would have realized that recursion is programmer friendly, not system because recursive version of a function is shorter to write, cleaner to see, and easier to maintain. And so, as it is said "anyone can write code that computers can understand, wise programmers write code that humans can understand." So keep coding with recursion. And yes, how long do you think the following program will take to finish its execution?
#include <stdio.h> long guessIt(int num) { if (num == 0) return 0; if (num == 1) return 1; return guessIt(num-1) + guessIt(num-2); } int main() { printf("num : guessIt(num)\n"); printf("=========================\n"); for (int num = 0; num < 100; num++) { printf("\n%3d: %d", num, guessIt(num)); } }
Last Word
In this tutorial we talked of recursion in C language and how does recursion work? Then types of recursion (linear, tail, binary, and multiple recursion), tracing recursive calls, and pros and cons of recursion. Hope you have enjoyed reading this tutorial. Please do write us if you have any suggestion/comment or come across any error on this page. Thanks for reading!
References
- Randal E. Bryant, David R. O'Hallaron, Computer Systems: A Programmer's Perspective
- Introduction to programming in Java
- Data Structures and Algorithms in Java (4th edition)

Share this page on WhatsApp